A Deep Dive into Latent Dirichlet Allocation (LDA) and Its Applications on Recommender Systems

Latent Dirichlet Allocation (LDA) is a topic modeling algorithm for discovering the underlying topics in corpora in an unsupervised manner. It has been applied to a wide variety of domains, especially in Natural Language Processing and Recommender Systems.

High-level point of view

LDA is a generative probabilistic model of a corpus/document. It is based on the “bag-of-words” assumption that words and documents are exchangeable. That is, the order of words within a document, or the orders of documents, are neglected. The basic idea is that every document is composed of a mixture of topics, whereas each topic is characterized by a distribution of words.

Every document is composed of a distribution of topics.

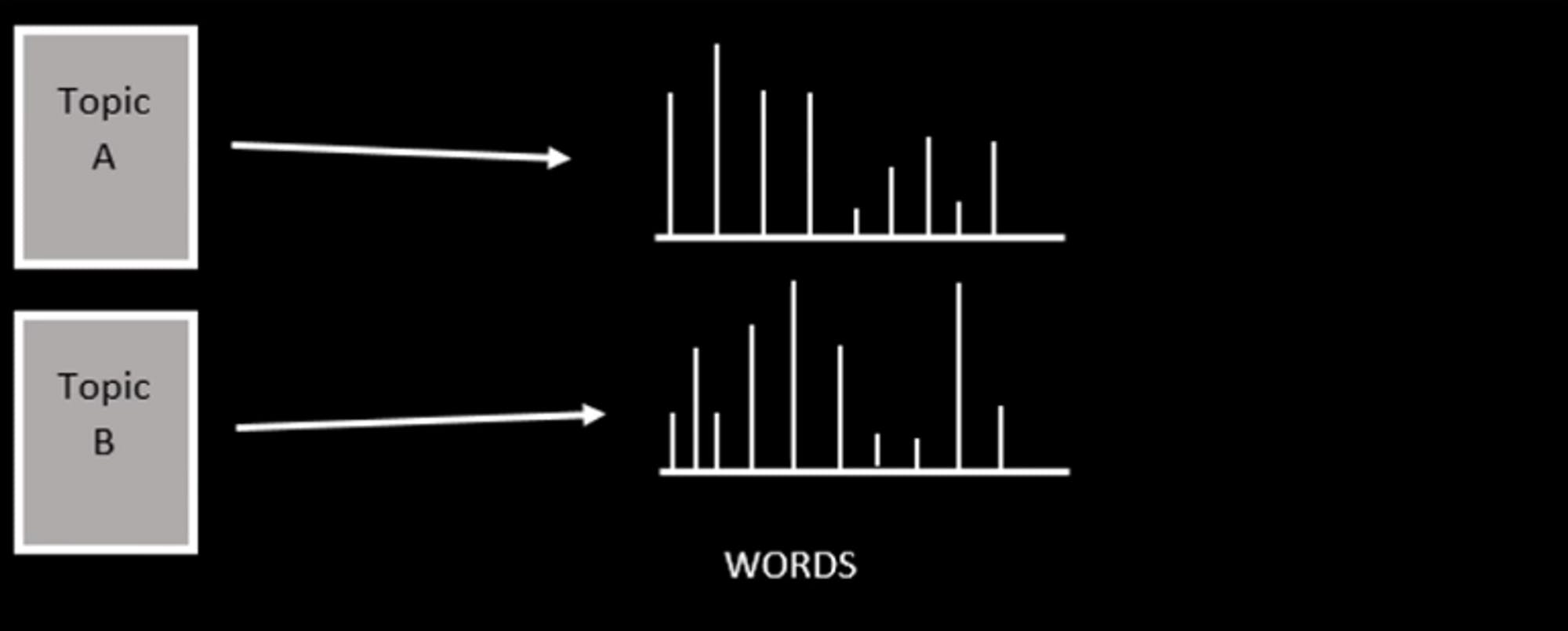
Each topic is characterized by a distribution of words

Check out this video to learn more about LDA Algorithm

-> https://www.youtube.com/watch?v=DWJYZq_fQ2A

LDA hypothesizes that every single document is generated by sampling the topics from each document followed by sampling words from each sampled topic. To obtain proper distribution of words and topics, we can train LDA with Gibbs Sampling, Maximum a Posteriori (MAP), or Expectation Maximization (EM).

Plate notation

To dive a bit deeper, let’s talk about the plate notation of LDA. In Bayesian inference, plate notation is a way of graphically expressing a repetitive process of sampling random variables. Each plate can be viewed as a “loop”, where as the variable shown in the bottom right corner of the plate represents the number of iterations of the loop. Below shows the plate notation of LDA.

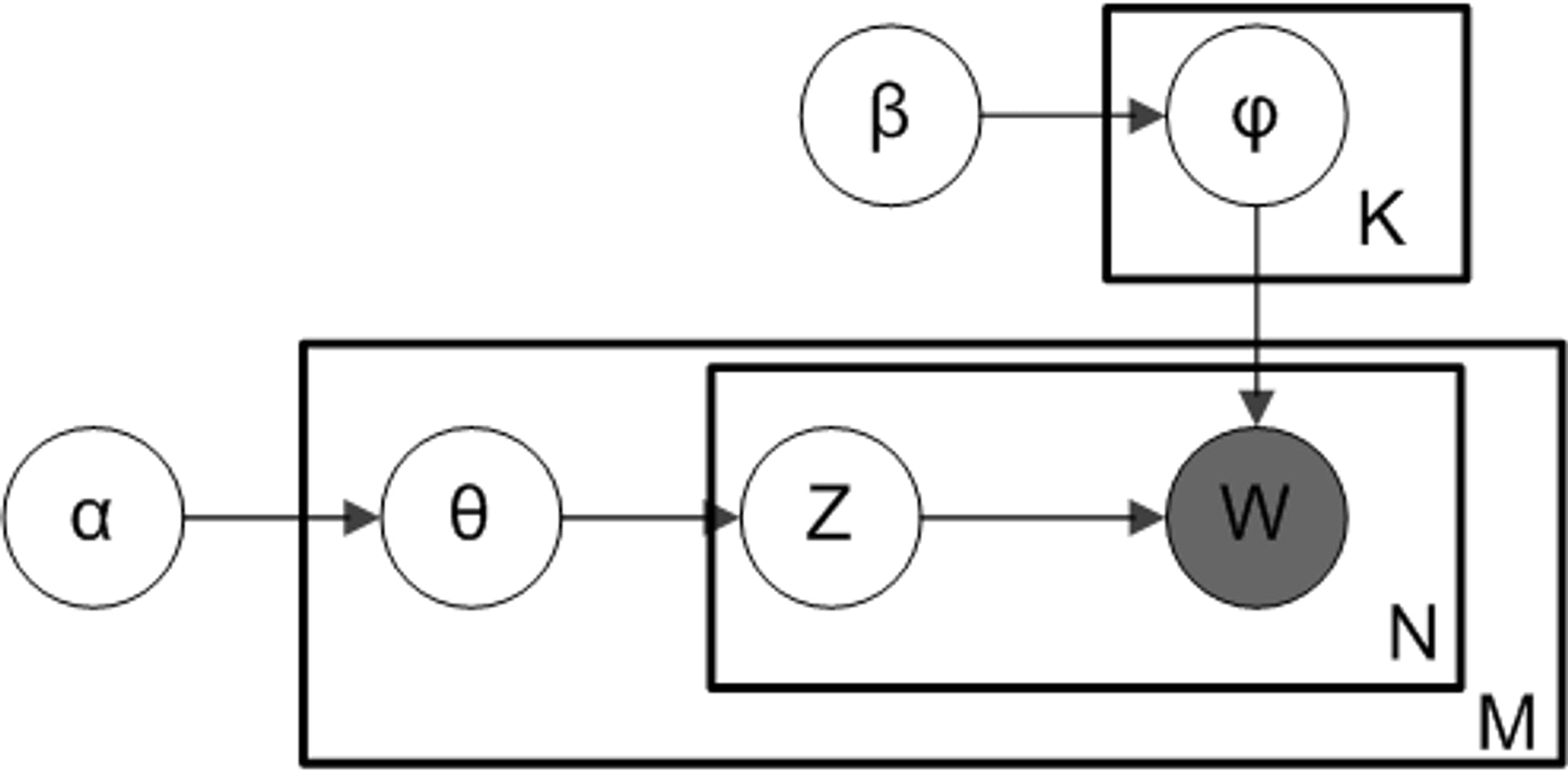
LDA plate notation

There are two components in the above diagram. The plate above states that there are K topics whose Dirichlet distribution over words is controlled by the hyper-parameter β. Similarly, the plate below describes that there are M documents, each of which contain N words. The circle colored in grey, w, is the observed word, while the circles represents different latent variables. z refers to the topic associated with w, and θ is the Dirichlet distribution of topics over documents, characterized by another hyper-parameter ⍺.

Generative process

Now that we understand roughly how documents are generated via plate notation. Let’s formulate it in mathematics.

1. Sample θ from a Dirichlet distribution θ_i ~ Dir(⍺) for i from 1 to M
2. Sample φ from another Dirichlet distribution φ_k ~ Dir(β) for k from 1 to K
3. sample z_ij ~ Multinomial(θ_i) and sample w_ij ~ Multinomial(φ_z_ij) for i from 1 to M, and for j from 1 to N:

Take The New York Times as an example. First, for each news article, we sample its topic distribution θ_i for the entire document as well as the word distribution φ_k over each topic. Secondly, for each ord j in the document, we draw a topic z_ij from the given topic distribution Multinomial(θ_i) followed by sampling a word based on the w_ij drawn from the given word distribution Multinomial(φ_z_ij). This process is visualized in the following figure.

Visualization of the generating process

https://docs.google.com/presentation/d/17vZ5kWGS8beROHHEKvXIcJN_d7KEBJ5TgAJCmKL1bkQ/edit?usp=sharing

Dirichlet distribution

We’ve been using Dirichlet as a black box without giving any explanation about it. Let’s briefly talk about the intuition behind Dirichlet distribution. A k-dimension Dirichlet distribution is controlled by a k-dimension parameter vector, Alpha. Below we show a 3 dimension example of Dirichlet distribution. The basic idea is that, the larger the alpha, the more the distribution get pushed to the center. This distribution enables the high flexibility of determining the portion of words/topics associated with a topic/document since some topics/ documents may be associated with a large group of words/topics, while the others may not.

Dirichlet Distribution

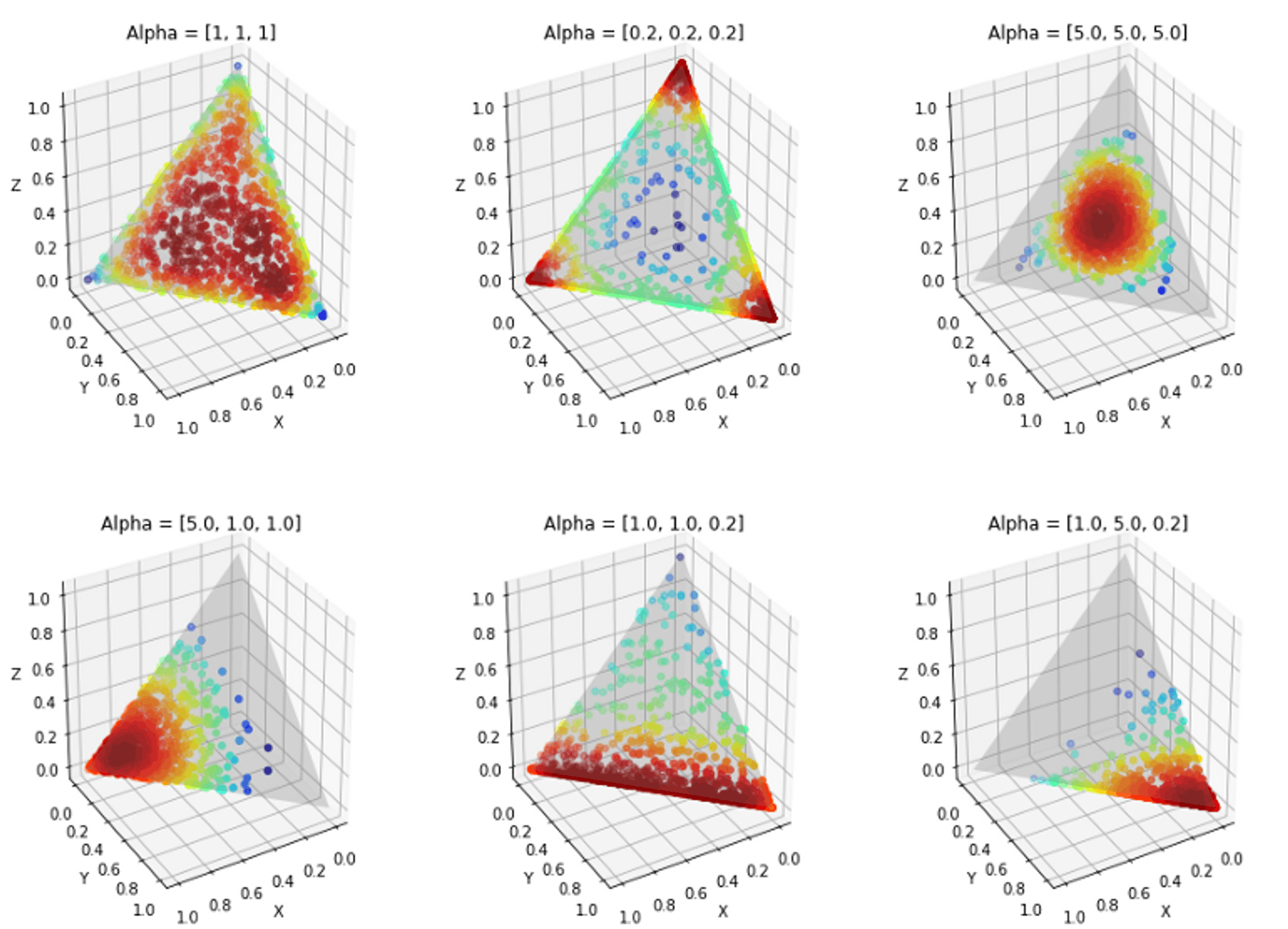
Learning

The problem of learning an LDA model is referred to as an “inference” problem. That is, given the observed variable, w, and the hyper-parameters ⍺ and β, how do we estimate the posterior of the latent variables.

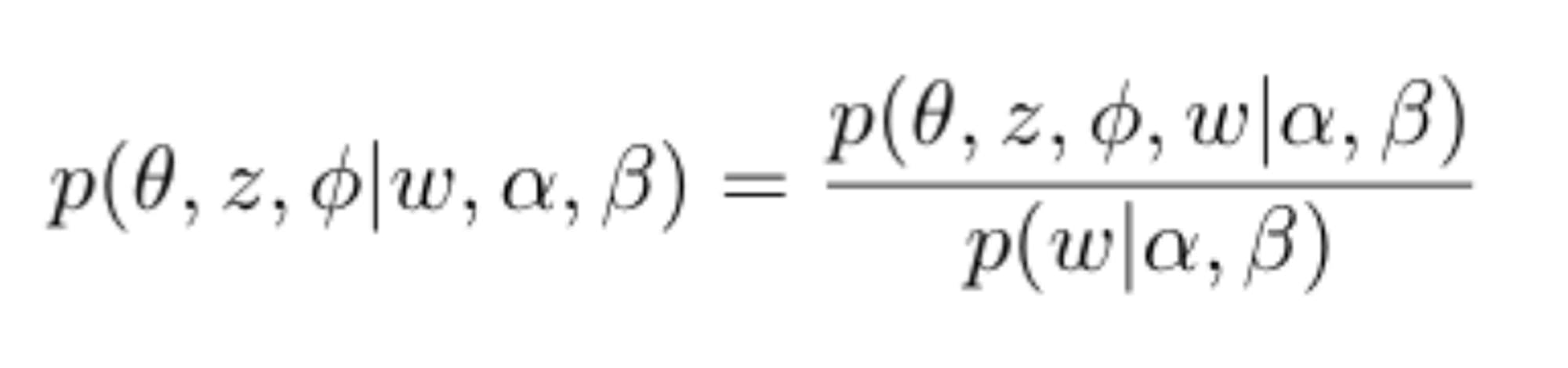
Yet, the integral for computing in the denominator is computationally intractable.

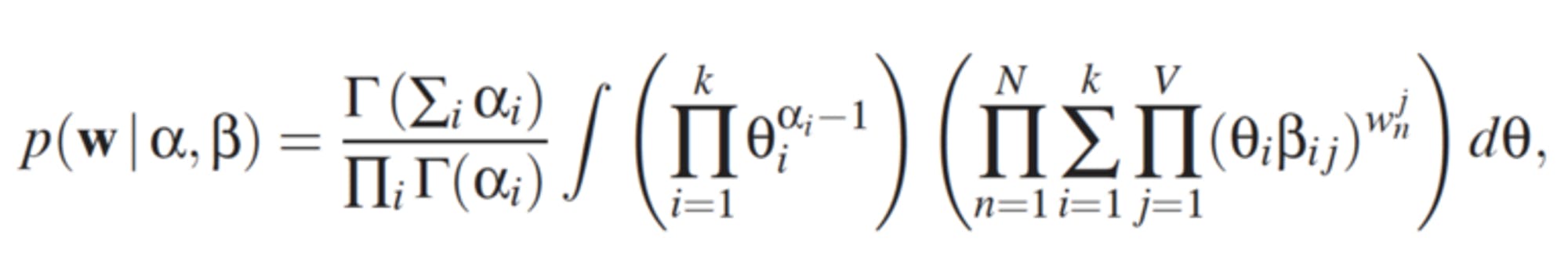
Therefore, approximate inference must be applied. Common approaches are Gibbs sampling and variational inference. In this post, we will focus on the former one.

Gibbs sampling

With Gibbs sampling, we can avoid directly computing the intractable integral. The basic idea is that we want to sample from p(w| ⍺, β) to estimate the distribution, but we cannot directly do so. Instead, Gibbs sampling allows us to iteratively compute the posterior of one of the latent variables while fixing all the other variables. This way, we can obtain the posterior distribution p(θ, z, φ| w, ⍺, β).

For each iteration, we alternatively sample θ, z, φ and with all the other variables fixed. The algorithm is shown in the following pseudo codes:

For i from 1 to MaxIter:

1. Sample θ_{i} ~p(θ | z= z_{i-1}, φ = φ_{i-1}w, ⍺, β)
2. Sample z_{i} ~p(z | θ =θ_{i}, φ = φ_{i-1}w, ⍺, β)
3. Sample φ_{i} ~p(φ | θ = θ_{i}, z= z_{i}w, ⍺, β)

Because the samples from the early iterations are not stable, we discard the first B iterations of samples, referred to as “burn-in”.

LDA on recommender system

LDA is typically used in recommender system for two contexts:

1. collaborative filtering (CF)
2. content-based recommendation

Collaborative filtering

When LDA is applied to item-based CF, items and users are analogous to documents and words that we have been talking about (user-based CF would be the opposite). In other words, each item is associated to a distribution over user groups (topics), and each user group is a distribution over users. With LDA, we can discover the hidden relationship between users and items.

Content-based recommendations

The second application is content-based recommendation, which is quite straight forward. Rather than merely leveraging plain TF-IDF to extract feature vectors the textual data for each item, we include LDA to model the topics of these textual data. A sample code for training LDA and inferencing the topics of a given document is provided below.

from gensim.test.utils import common_texts
from gensim.corpora.dictionary import Dictionary
from gensim.models import LdaModel

# Create a corpus from a list of texts
common_dictionary = Dictionary(common_texts)
common_corpus = [common_dictionary.doc2bow(text) for text in common_texts]

# Train the model on the corpus.
lda = LdaModel(common_corpus, num_topics=10)

Train LDA

# infer the topic distribution of the second corpus.
lda[common_corpus[1]]
'''
output
[(0, 0.014287902),
 (1, 0.014287437),
 (2, 0.014287902),
 (3, 0.014285716),
 (4, 0.014285716),
 (5, 0.014285714),
 (6, 0.014285716),
 (7, 0.014285716),
 (8, 0.014289378),
 (9, 0.87141883)]
'''

Inference topic distribution vectors

Conclusion

In this blog post, we have discussed LDA from high-level to detailed mathematical explanation. In addition, we have talked about the application of LDA on Recommender Systems and provided you sample codes on how to use it. I hope you find this article helpful and till next time :)

References

1. Blei, D. M., Ng, A. Y., & Jordan, M. I. (2003). Latent dirichlet allocation. Journal of machine Learning research, 3(Jan), 993–1022.
2. Alexander, S. Latent-Variable Modeling for Natural Language
3. Scott, S LDA Algorithm Description
4. Thushan, G. Intuitive Guide to Latent Dirichlet Allocation